1 3 And 3 1 Matrix Multiplication

Matrix Multiplication: Example 3 (3x3 by 3x1). 3.6.1.3 Solution in Terms of Reflection-Coefficient Matrices. A direct propagator-matrix multiplication approach is not always reliable for solving the obtained equation system (cf. Section 3.3.4.2). The direct global matrix method is applied in Ref. The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one. As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the same quantity of columns as the 2nd one. Matrix Multiplication (1 x 3) and (3 x 1) Multiplication of 1x3 and 3x1 matrices is possible and the result matrix is a 1x1 matrix. This calculator can instantly multiply two matrices and show a step-by-step solution. Rows: Columns: + − ×. Rows: Columns: ×.
- Related Questions & Answers
- Selected Reading
A matrix is a rectangular array of numbers that is arranged in the form of rows and columns.
An example of a matrix is as follows.
A 3*2 matrix has 3 rows and 2 columns as shown below −
A program that performs matrix multiplication is as follows. Kite compositor animation and prototyping 2 0 1.
Example
Output
In the above program, the two matrices a and b are initialized as follows −
If the number of columns in the first matrix are not equal to the number of rows in the second matrix then multiplication cannot be performed. In this case an error message is printed. It is given as follows.
Both the matrices a and b are displayed using a nested for loop. This is demonstrated by the following code snippet.
After this, the product[][] matrix is initialized to 0. Then a nested for loop is used to find the product of the 2 matrices a and b. This is demonstrated in the below code snippet.
Creativemarket editorial magazine lightroom presets download free. After the product is obtained, it is printed. This is shown as follows.
A Matrix is an array of numbers:
A Matrix
(This one has 2 Rows and 3 Columns)
To multiply a matrix by a single number is easy:
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Fix a flat modern tech grooves acid download free. We call the number ('2' in this case) a scalar, so this is called 'scalar multiplication'.
Multiplying a Matrix by Another Matrix
But to multiply a matrix by another matrix we need to do the 'dot product' of rows and columns . what does that mean? Let us see with an example:
To work out the answer for the 1st row and 1st column:
The 'Dot Product' is where we multiply matching members, then sum up:
(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
We match the 1st members (1 and 7), multiply them, likewise for the 2nd members (2 and 9) and the 3rd members (3 and 11), and finally sum them up.
Want to see another example? Here it is for the 1st row and 2nd column: Torrent wham the final torrent.
(1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
We can do the same thing for the 2nd row and 1st column:
(4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
And for the 2nd row and 2nd column:
(4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154 https://couponsoftware.mystrikingly.com/blog/brave-32-bit.
And we get:
DONE!
Why Do It This Way?
This may seem an odd and complicated way of multiplying, but it is necessary!
Allegorithmic substance painter 2019 3 2 download free. I can give you a real-life example to illustrate why we multiply matrices in this way.
Example: The local shop sells 3 types of pies.
- Apple pies cost $3 each
- Cherry pies cost $4 each
- Blueberry pies cost $2 each
And this is how many they sold in 4 days:
Now think about this . the value of sales for Monday is calculated this way:
So it is, in fact, the 'dot product' of prices and how many were sold:
($3, $4, $2) • (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
How to turn rar files into package. We match the price to how many sold, multiply each, then sum the result.
In other words:
- The sales for Monday were: Apple pies: $3×13=$39, Cherry pies: $4×8=$32, and Blueberry pies: $2×6=$12. Together that is $39 + $32 + $12 = $83
- And for Tuesday: $3×9 + $4×7 + $2×4 = $63
- And for Wednesday: $3×7 + $4×4 + $2×0 = $37
- And for Thursday: $3×15 + $4×6 + $2×3 = $75
So it is important to match each price to each quantity.
Now you know why we use the 'dot product'.
And here is the full result in Matrix form:
They sold $83 worth of pies on Monday, $63 on Tuesday, etc.
(You can put those values into the Matrix Calculator to see if they work.)
Rows and Columns
To show how many rows and columns a matrix has we often write rows×columns.
Example: This matrix is 2×3 (2 rows by 3 columns):
When we do multiplication:
- The number of columns of the 1st matrix must equal the number of rows of the 2nd matrix.
- And the result will have the same number of rows as the 1st matrix, and the same number of columns as the 2nd matrix.
Example:
In that example we multiplied a 1×3 matrix by a 3×4 matrix (note the 3s are the same), and the result was a 1×4 matrix.
In General:
To multiply an m×n matrix by an n×p matrix, the ns must be the same,
and the result is an m×p matrix.
So . multiplying a 1×3 by a 3×1 gets a 1×1 result:
3 By 1 Multiplication Worksheet
But multiplying a 3×1 by a 1×3 gets a 3×3 result:
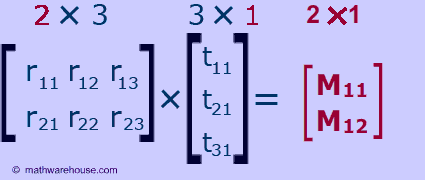
Identity Matrix
The 'Identity Matrix' is the matrix equivalent of the number '1':
A 3×3 Identity Matrix
- It is 'square' (has same number of rows as columns)
- It can be large or small (2×2, 100×100, . whatever)
- It has 1s on the main diagonal and 0s everywhere else
- Its symbol is the capital letter I
It is a special matrix, because when we multiply by it, the original is unchanged:
A × I = A
I × A = A

Order of Multiplication
In arithmetic we are used to:
3 × 5 = 5 × 3
(The Commutative Law of Multiplication)
But this is not generally true for matrices (matrix multiplication is not commutative):
AB ≠ BA
When we change the order of multiplication, the answer is (usually) different.
Example:
3 Digit Multiplication By 1
See how changing the order affects this multiplication:
0 And 1 Multiplication Practice
3 By 2 Matrix
The answers are different!
2 And 3 Multiplication Worksheets
It can have the same result (such as when one matrix is the Identity Matrix) but not usually.

1 3 And 3 1 Matrix Multiplication
UNDER MAINTENANCE